「プロスペクト理論」って、わかるようなわからないような感じですよね。「人間は損失に敏感って話だっけ?」くらいの印象ではないでしょうか?
プロスペクト理論は、その他の細かい理論に派生していますが、根っこは全て同じです。プロスペクト理論をキチンと理解しているだけで、ビジネスでは強力な武器になります。
そんな「プロスペクト理論」のエッセンスを、凝縮してひとつの記事にしました。この記事では次のことがわかります。
- プロスペクト理論とは何か?(具体例と図で解説)
- プロスペクト理論を仕事に活かす思考法
- プロスペクト理論をさらに活かすための6つの派生理論
難しい用語は極力排除しているので、初見の人でも理解しやすい内容になっています。この記事を読むだけで、全ビジネスパーソンの必須知識が手に入ります。
今すぐチェックしましょう!
プロスペクト理論とは?

プロスペクト理論(prospect-theory)とは…
不確実性下(リスクがある状況)における人間の意思決定をモデル化した理論です。
行動経済学でもっとも有名な理論の一つです。
これだけだとわかりづらいので、もう少し噛み砕きましょう。
- ギャンブルは、勝つときもあれば、負けるときもあります
- 新しいレストランに行けば、当たりもあれば、ハズレもあります
- 株式投資は、利益が出るときも、損失が出るときもあります
という風に、人間の選択と行動の結果に「絶対」はありません。「確率」によって利得か損失のどちらかが発生します。
このような、「確率」によって利得や損失が発生する状況で、人間がどのように意思決定をしているかを説いたのが「プロスペクト理論」です。
プロスペクト理論の3原則

「プロスペクト理論」は、3つの心理作用を組み合わせて、1つの汎用的な理論に練り上げられたものです。
すなわち次の3つです。
プロスペクト理論の3原則
- 損失回避性
- 感応度逓減性
- 参照点依存性
この3つの心理作用を1つにまとめた下記の関数が、「プロスペクト理論」の全容です。
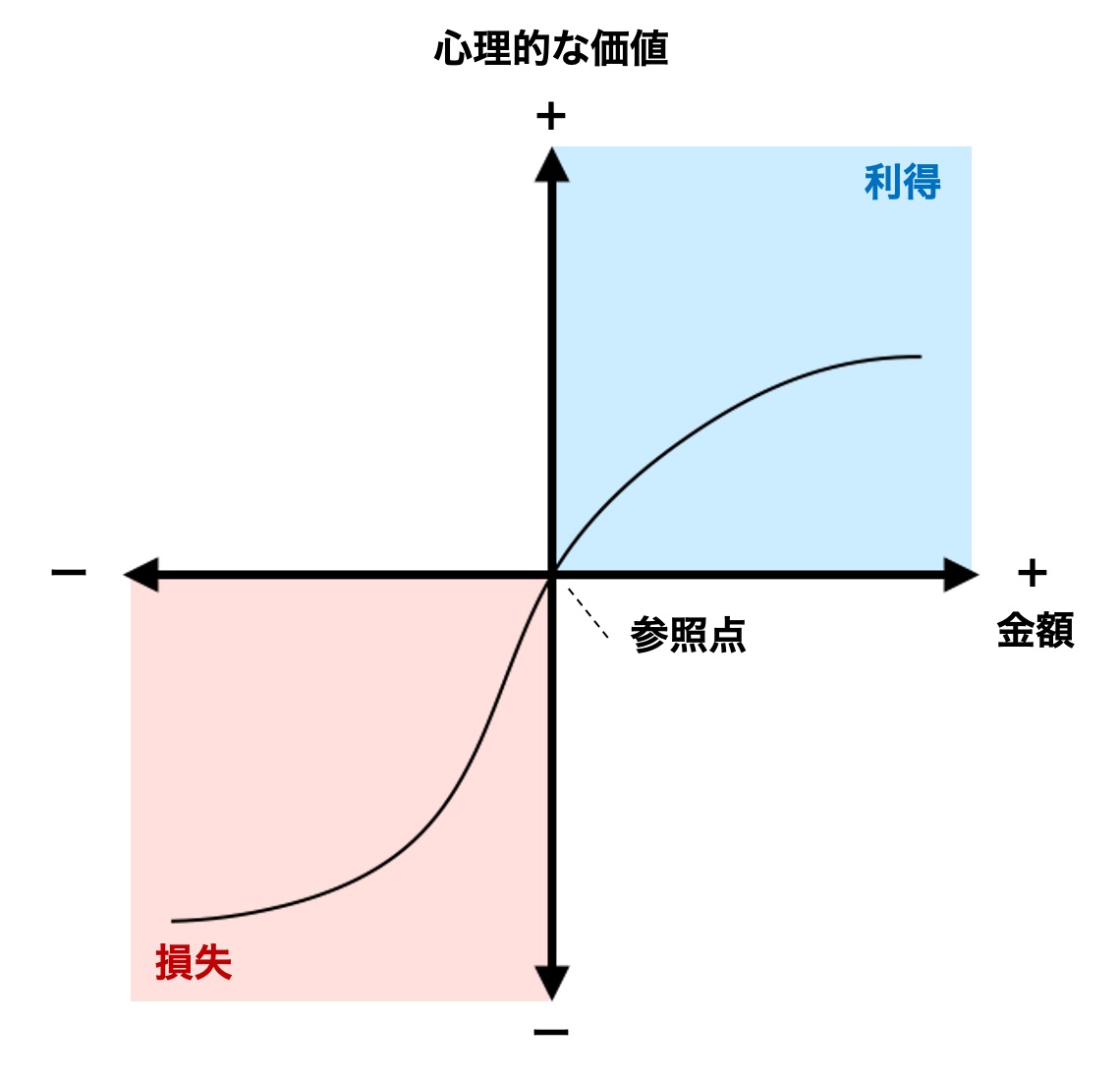
この関数だけ見ても、何のこっちゃよくわからないですね。
それぞれの特徴を、例と図を使ってわかりやすく解説していきます。
原則①:損失回避性
損失回避性とは…
「利益」から得られる満足より、同額の「損失」から得られる苦痛の方が大きいために、「損失」を「利益」より大きく評価する心理現象のことです。
一般的には人間の脳は、何かを得る喜びより、何かを失う悲しみの方が2倍ほど大きく感じると言われています。
「損失回避性が」プロスペクト理論の出発点になっています。これだけでも使えるシーンがたくさんあるので、ぜひ覚えておきましょう。
損失回避性の例
次の問題を考えてみてください。
- コインを投げて、表だったら1万円もらえる。
- 裏だったら逆に1万円を払わなければならない。
どうでしょう?あなたは、このギャンブルを受けますか?
実は多くの人は、このギャンブルを割りに合わないと思って受けません。あなたも直感的にそう思ったのではないでしょうか?
その理由は、すでに先ほどの関数で表現されています。曲線の傾きがポイントです。
このギャンブルの収支に当たる「+1万円」と「−1万円」を関数に当てはめてみましょう。
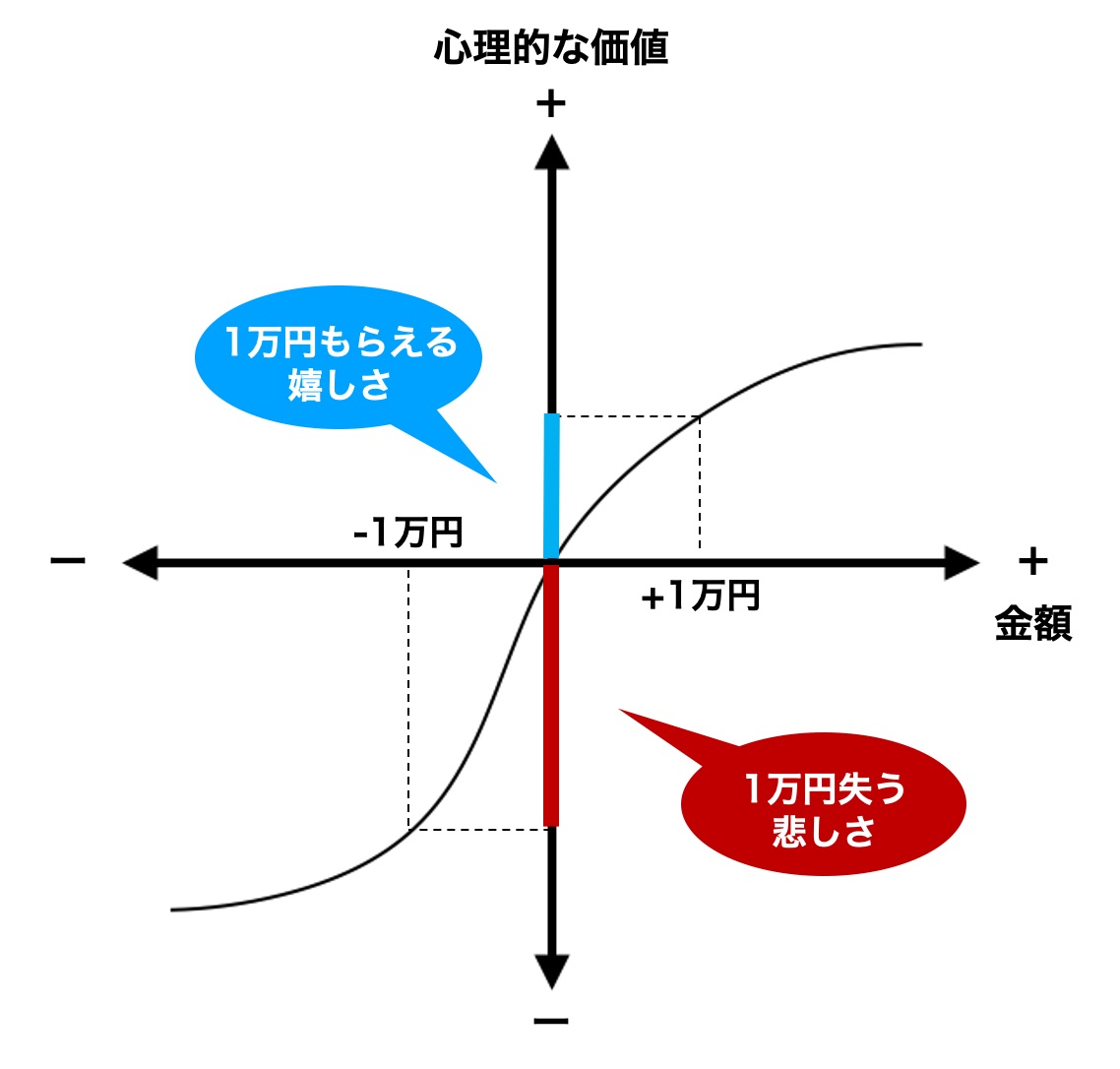
「利益を得るときの曲線」より、「損失を被るときの曲線」の方が傾きが大きいことがわかりますね。
「新たに1万円得られる嬉しさ」<「今持っている1万円を失う悲しさ」になっていますね。
数字上の期待値は0ですが、心理的な期待値はマイナス(悲しさの方が大きい)になってしまいます。そのため、この賭けは割りに合わないと判断されます。
このような賭けでは、「利益」が「損失」より1.5倍〜2.5倍程度大きくないと、ほとんどの人が賭けに乗ってくれません。
行動経済学っぽく言えば、「確率によって損得の両方が起こりうる賭けでは、損失を回避するためにリスク回避的な行動をとる」です。
原則②:感応度逓減性
感応度逓減性とは…
「利得」「損失」の絶対値が大きくなるにつれて、「嬉しさ」「悲しさ」の感覚が鈍っていく現象です。
これは非常にカンタンな話です。
次の2人をイメージしてみてください。
- Aさん:貯金300万円の人が100万円もらう
- Bさん:貯金1,000万円の人が100万円もらう
両者の嬉しさは違いますよね。
貯金300万円のAさんの方が、ずっと嬉しいと思うでしょう。
これも関数で表現されています。あらためて関数の図を見てみてください。

曲線がS字型になっていて、傾きが徐々に緩やかになっています。嬉しさ・悲しさの増分が徐々に小さくなっているのがわかりますね。
感応度逓減性の例①:得する賭けは「リスク回避的」に
次の問題を考えてみてください。
次の2つのゲームのいずれかを選べます。どちらを選びますか?
- A:コインを投げて、表が出たら100万円もらえるが、裏が出たら1円ももらえない
- B:確実に50万円もらえる
数字の上での期待値はどちらも50万円で一緒。ですがほとんどの人は、「B:確実に50万円もらえる」を選択します。
この現象も同じ関数で説明できます。
このゲームのリターンである「50万円」と「100万円」を関数に当てはめてみましょう。
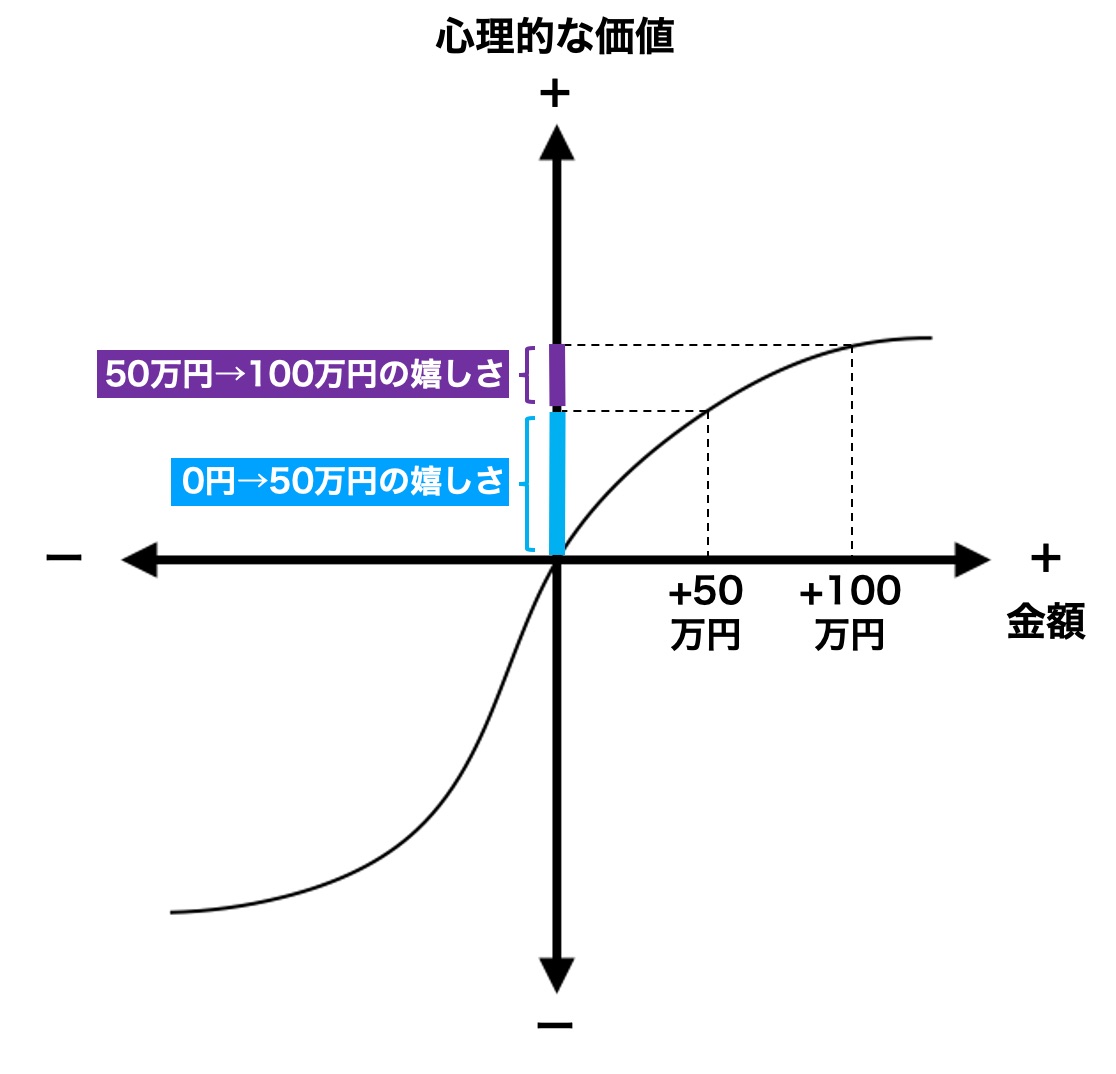
「0円→50万円の嬉しさ」>「50万円→100万円の嬉しさ」になっていますね。
数字の上での期待値はどちらも一緒ですが、心理的な期待値は「確実にもらえる50万円」の方が大きいことになります。
一か八かで100万円を狙うよりも、確実な50万円で妥協した方が、満足度のコスパがいいわけですね。
行動経済学では、このような意思決定の仕方を、「リスク回避的な行動をとる」と言います。
身近な例
- 麻雀をやったことがある人ならわかると思います。勝っているときほどリスクを避け、安い手で確実にあがろうとします。
- 株式投資をしている人は、利益が出たら、その先また下がるともわからないので、とりあえず売却して利益確定したい衝動に駆られます。
直感的にも理解できる内容かなと思います。
感応度逓減性の例②:損する賭けは「リスク追求的」に
次の問題を考えてみてください。
先ほどの問題では「貰える」だったところが、「払う」に変わっています。
次の2つのゲームのいずれかを選べます。どちらを選びますか?
- A:コインを投げて、裏が出たら100万円払わなければならないが、表が出たら1円も払わなくてよい
- B:確実に50万円払う
こちらも数字上の期待値はどちらもマイナス50万円で同じ。
ですが今度は、ほとんどの人が、「A:裏が出たら100万円払わなければならないが、表が出たら1円も払わなくてよい」を選びます。
このゲームのマイナスである「−50万円」と「−100万円」を関数に当てはめてみましょう。
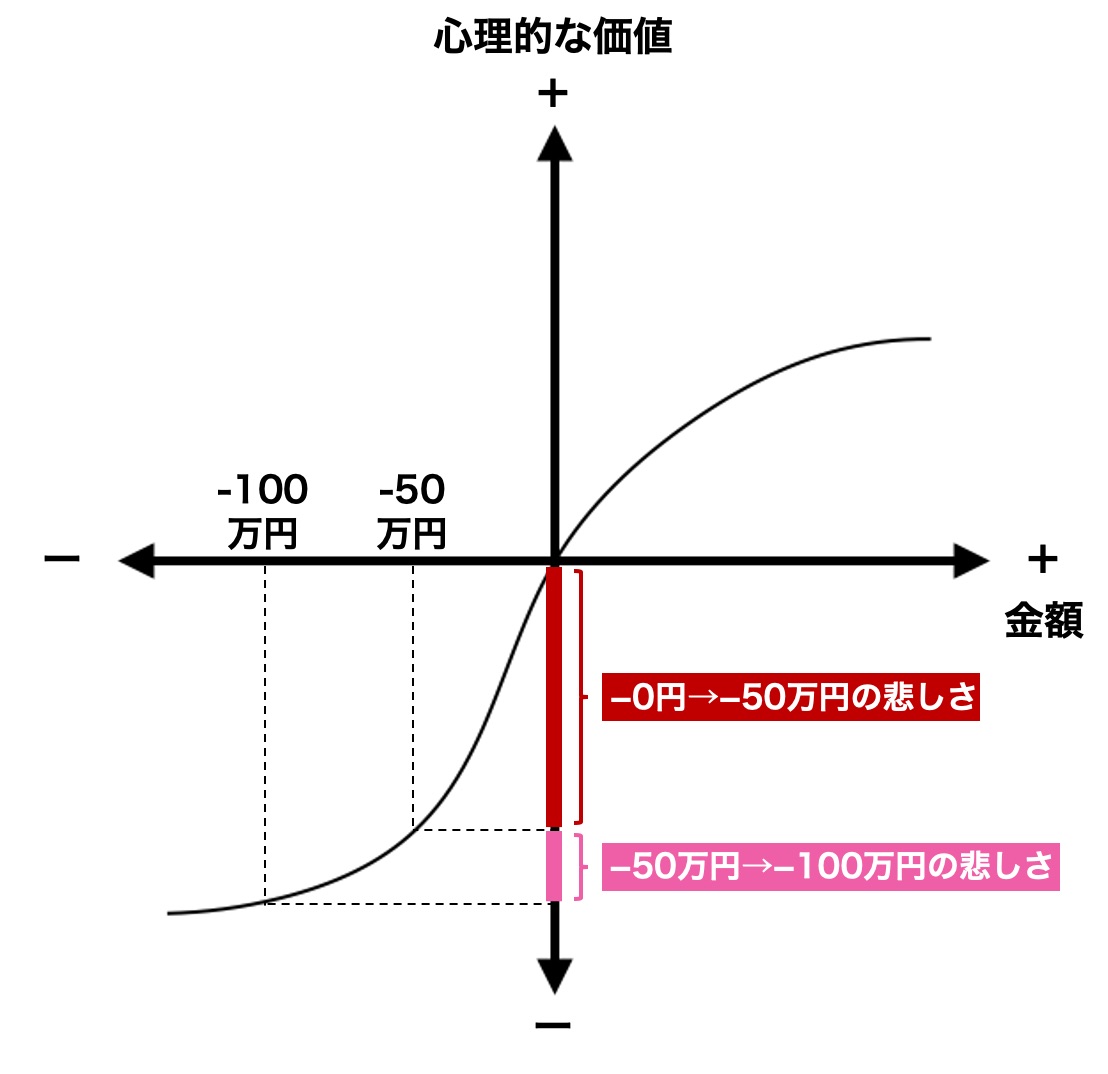
「0円→−50万円の悲しさ」>「−50万円→−100万円の悲しさ」になっていますね。
数字の上での期待値はどちらも一緒ですが、心理的な期待値は「確実に失う50万円」の方がマイナスが大きい(辛い)ことになります。
−50万円の損失が確定する選択肢を選ぶと、大きな悲しみが確定してしまいます。
それならば1/2の確率で悲しさを0にしたいと考えます。もし賭けに負けても、−50万円が−100万円になって増える悲しみは比較的小さいからです。
行動経済学では、このような意思決定の仕方を、「リスク追求的な行動をとる」と言います。
身近な例
- 麻雀で負けが込んでいる人は、リスクのある牌を切ってでも、高い役で上がろうとしがちです。
- 株式投資している人は、値下がりした株を売却すると損失が確定してしまいます。株価上昇を期待して、売却せずに持ち続けてしまいます。
こちらも「なるほど」と頷ける内容ではないでしょうか。
原則③:参照点依存性
参照点依存性とは…
ある地点の数値を基準として、その基準値からの変化で損得の判断をすることです。
「損」か「得」かの判断は、必ずしも「0」を境目にするわけではありません。
営業ノルマを想像するとわかりやすいですね。ノルマは営業成績の基準値で、ノルマのバーを上回れば「得」になり、下回れば「損」になります。
関数の中心点が、参照点にあたります。何のこっちゃよくわからないと思いますが、次の例を見てもらえれば納得いただけると思います。
参照点依存性の例
次の問題①②をそれぞれ考えてみてください。
まず、はじめに100万円もらえます。
その上で次の2つのゲームのいずれかを選べます。どちらを選びますか?
- A:50%の確率でさらに100万円もらう
- B:確実に50万円もらう
まず、はじめに200万円もらえます。
その上で次の2つのゲームのいずれかを選べます。どちらを選びますか?
- A:50%の確率で100万円払う
- B:確実に50万円払う
この問題に直面したほとんどの人は、
- 問題①の回答 → B:確実に50万円もらう
- 問題②の回答 → A:50%の確率で100万円払う
を選びます。
種明かしをしてしまうと、問題①と問題②で、選択肢Aはどちらも同じ結果になります。選択肢Bも同様です。
- Aの結果:50%の確率で200万円か100万円をもらう
- Bの結果:確実に150万円もらう
問題文の書きっぷりが異なるだけで、内容は同じなのです。
問題の表現がちょっと違うだけで、多くの人の意思決定が変わってしまいます。
この現象のカラクリは、2つの問題は結果が同じでも、参照点が異なるところにあります。参照点が「100万円」か「200万円」かによって、別の問題として捉えられています。
関数の参照点を「100万円」「200万円」にして、それぞれの問題をおさらいしましょう。
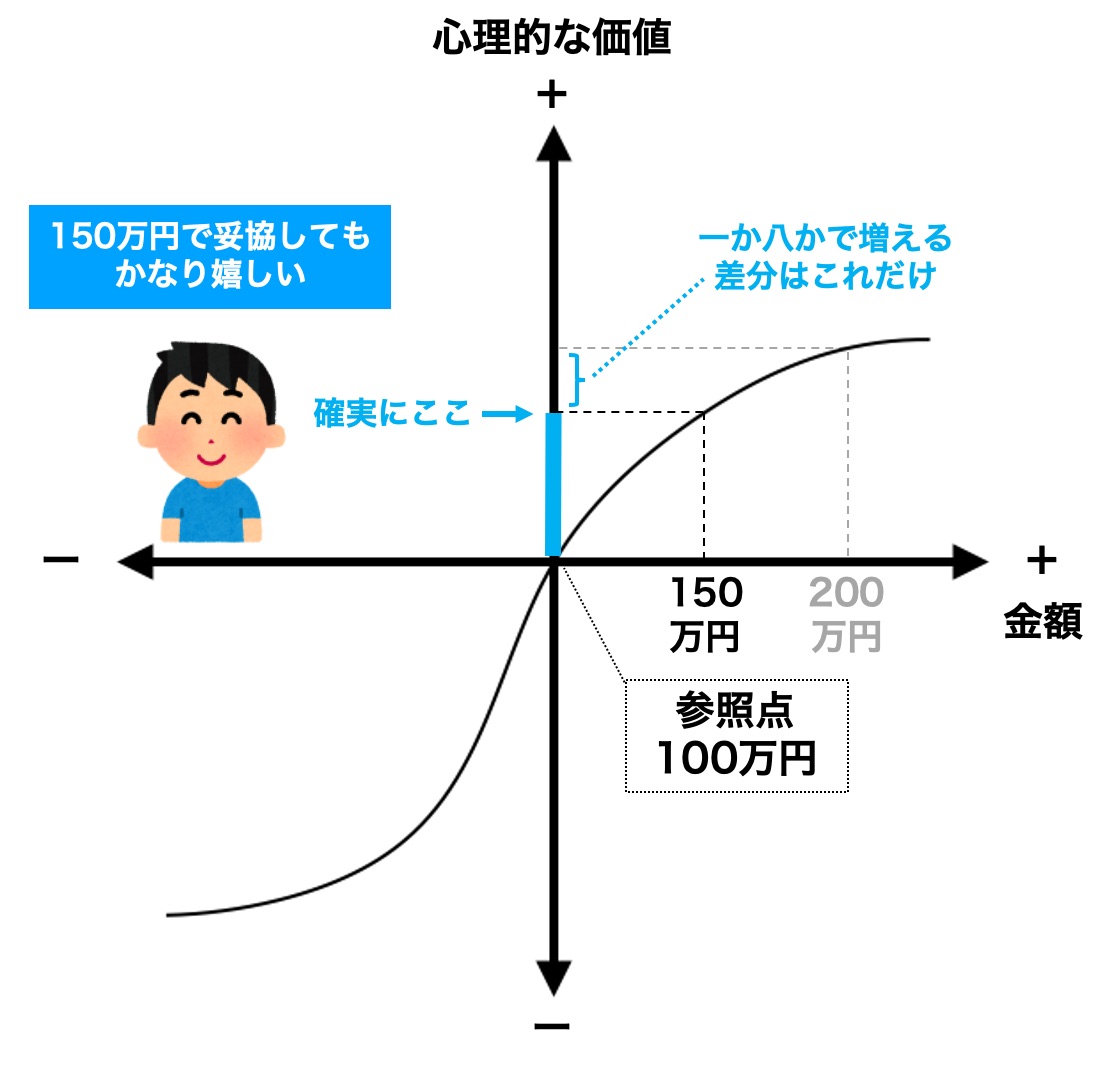
問題①は、「100万円」が参照点なので、「150万円」も「200万円」も利得として捉えられます。
「感応度逓減性」により、確実に「150万円」をゲットする選択肢を選びます。「150万円」と「200万円」では、嬉しさに大差ないからです。
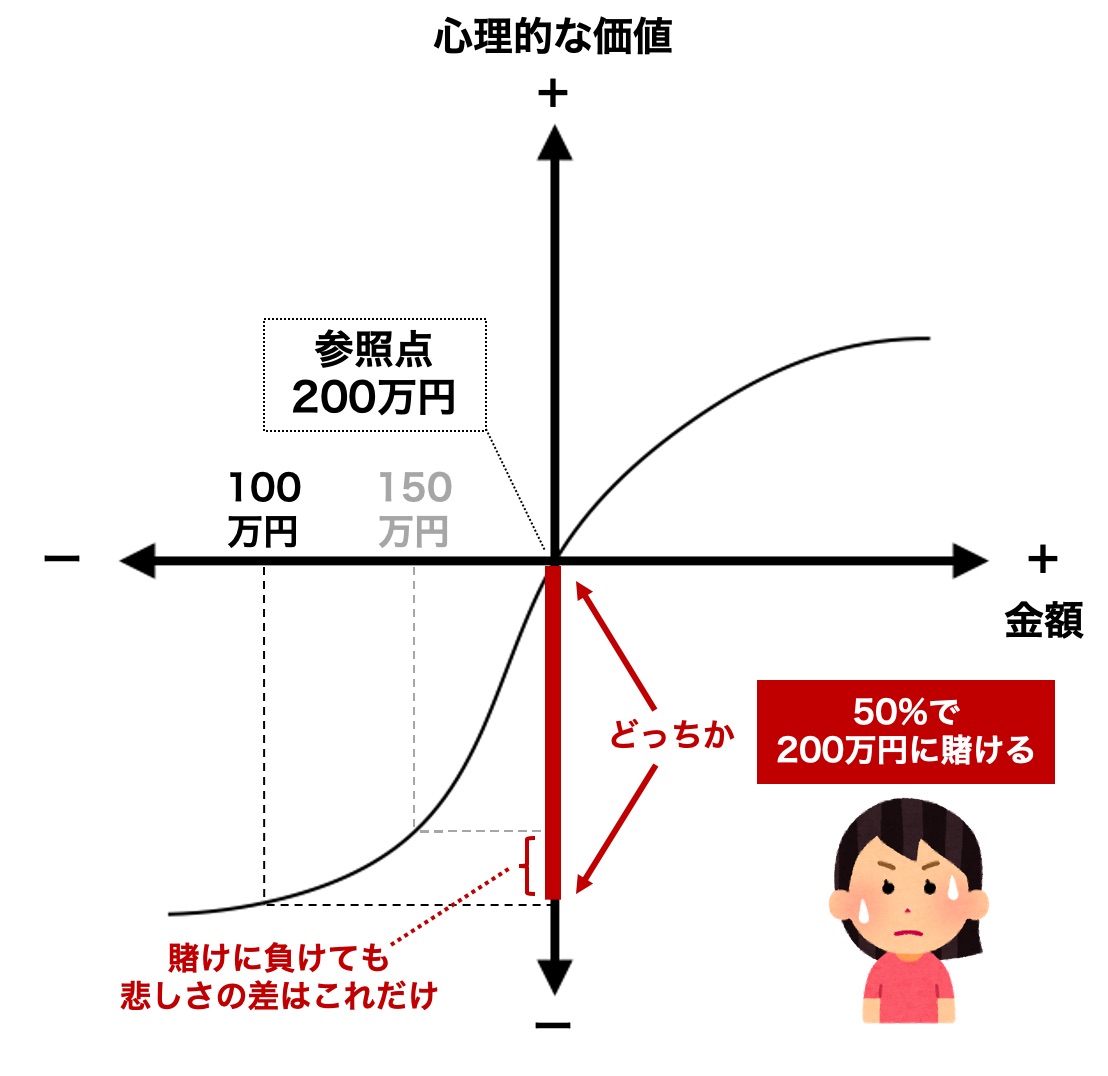
一方で問題②は、参照点が「200万円」です。「150万円」と「100万円」は損失と見なされます。
「損失回避性」により、「150万円」に下がったときは大きな悲しみが発生します。ただし、「感応度逓減性」により、「150万円」から「100万円」に下がったときの悲しみの増分はグッと抑えられます。
そのため、確実に悲しみを背負うよりも、一か八かで「200万円」を狙います。
ゴルフのパーはわかりやすい参照点です。ボギーは「損失」で、バーディは「利得」になります。*ボギーは基準打数(パー)より1打多い、バーディは1打少ないの意味です。
「パー」になるか「ボギー」になるかの場面の方が、「パー」になるか「バーディ」になるかの場面より成功率が高いという調査結果があります。
パーという参照点に対し、損失となるボギーを必死で回避しようとしているからです。
身近な例
- 麻雀は3万点返しルールが多いと思うので、参照点は3万点になります。
- 株は購入したときの金額が参照点になります。
以上の3つの原則で、「プロスペクト理論」の中身は押さえられました。お疲れ様でした。
おそらく理解はしてもらえたと思いますが、情報量が多かったので、頭がいっぱいいっぱいになっているかもしれません。ぜひ繰り返し見て、腹落ちさせてくださいね。
続いて、実生活にどのように生かしていくかを解説していきます。
プロスペクト理論を仕事に活かす思考法 4選

「プロスペクト理論」は汎用的な概念なので、活用方法を細かく書くとトンデモない文章量になってしまいます。ぜひあなたの文脈で考えてみてください。
ここでは「プロスペクト理論」を使った思考法を紹介します。みなさんが直面する具体的なシーンに当てはめて使ってみてください。
思考法①:この1回だけではなく、何回もあるうちの1回と考える
選択が「1回」しかないのであれば、損失回避的になるのは致し方ありません。
例えば次の賭けに乗る人は、そうそういないでしょう。
50%の確率で2億円得られるが、50%の確率で1億円の借金を背負うゲーム
期待値は+5,000万円なので、理論上は勝負すべき。ですが、リスクが高過ぎますね。
でも、そのチャンスが「1,000回」あるとしたらどうでしょう?
「大数の法則」により、回数が多くなるほど、リターンは期待値に収束していきます。1,000回やれば、ほぼほぼ確実に+約5,000万円を手にできるでしょう。
勝負しないなんて考えられませんね。
優秀なトレーダーは、そのように考えて株の売買を行います。見込みの薄い株は損切りし、調子のいい株は長期保有します。様々なことに同じ思考法を適用できます。
複数事業を持つ企業なら、全ての事業を石橋を叩いて渡るのではなく、思いっきりチャレンジしても良いでしょう。
いくつかの事業が失敗しても、どれかが成功すれば元が取れます。ベンチャーキャピタルは、この思想で多数のベンチャーに投資をしています。
人付き合いでも同じです。100人に1人だけ酷い人がいて、失敗の経験をしてしまった過去があったとします。
その経験から他人を一切信用しないようになったとしたら、他の99人と築けたはずの友好な関係まで捨てることになります。そんな生き方はトータルで見れば損です。
選択肢を選ぶときは、その1回きりではなく、この先に幾度も訪れる機会のトータル回数で考えましょう。1回のミスを恐れすぎると、好機を逃してトータルでは損してしまうかも。
思考法②:損失を強調して伝える
人間の感情は、「得」するよりも「損」する方に2倍敏感です。
というわけで、「利得」を強調するより、「損失」を強調した表現にした方が、相手の感情を揺さぶることができます。
- 先着10名までです。当日は混雑が予想されます。
- 明日以降は、通常価格での販売となります。
- 今月末で、2,000ポイント失効します。
といった具合に、行動しないと「損」することをアピールしましょう。より訴求力のあるメッセージになります。
誰かを説得したり、提案したり、キャッチコピーを考えたりするときに応用できます。
思考法③:不安からビジネスチャンスを見出す
「不安を感じていない人」や「不安に気がついていない人」に、不安を感じさせると、そこにビジネスチャンスが生まれます。
人間の感情が損失に大きく揺さぶられるとしたら、損失を埋めるビジネスには強い魅力があることになるからです。
無料カウンセリングやちょっとした診断サービスを提供して、消費者の不安を煽ってみましょう。広告よりも強いはるかに強い効果が期待できるはずです。
思考法④:目標値を定める
自分でも他人でも、行動させたいことがあるなら、「参照点(目標値)」を作りましょう。
「損」か「得」かの判断は、参照点を上回っているか下回っているかによって決まります。
参照点を下回っていれば「損失」と見なされます。「損失」の状況では、なんとか参照点まで追いつこうと頑張ります。
- 1日8時間までしか働かない
- 年収1,000万円
- 月に10冊本を読む
といった具合に、目標を定めましょう。
達成できなかった分はマイナス(損失)の感情になるので、達成のための強いモチベーションが生まれます。
プロスペクト理論から派生した理論 6選

「プロスペクト理論」から、多数の行動経済学の理論が派生しています。日常生活・ビジネス・資産運用など、活用の幅は多岐に渡ります。
ここでは6つの派生理論を紹介します。
プロスペクト理論からの派生理論
- フレーミング効果
- サンクコスト効果
- 保有効果
- 現状維持バイアス
- 確実性効果
- メンタルアカウンティング
「プロスペクト理論」は汎用的なので、個々の理論の方が実生活に当てはめて考えやすいかもしれません。サラッと概要を触れていくので、詳細は個別の記事を見てみてください。
派生①:フレーミング効果
フレーミング効果とは…
実際には同じ意味であっても、表現の仕方が変わるだけで、受け取る人の印象が真逆になってしまう現象のこと。
例えば、次の2つは全く同じ意味ですが、受け取る印象は随分異なります。
- A:手術が成功して完治する可能性は90%です。
- B:手術が失敗して死亡する可能性は10%です。
「損失回避性」により、損失を強調した「B」の文章を聞かされた人は、「A」を聞かされた人よりも、手術を承諾しづらくなります。
ビジネスに応用する場合は、「今ならキャンペーンで1,000円お得!」よりも「今買わないと1,000円高くなります」の方が効果的なコピーになります。
≫ 【言いかえるだけで売れる】フレーミング効果とは?具体例で解説

派生②:サンクコスト効果
サンクコスト効果とは…
あるものに対し、時間や費用を投資し続けることが損失につながる可能性が高いのに、「もったいないから」と感じてやめられなくなってしまう現象のこと。
「損失回避性」により、これまで費やしたお金や時間がムダになり、損失が確定する状況に強い嫌悪感を覚えます。
サンクコスト効果の例
- 買った本が面白くなくても最後まで読んでしまう
- 長年課金し続けてきたソシャゲがやめられない
- Amazonプライムをサブスク契約でお金払っているので、せっかくだからAmazonで買う
株の損切りができない現象は、サンクコスト効果の典型的な症状です。購入価額を下回っても、売却しなければ損失は確定しません。
だから損切りできずに、見込みのない株を持ち続けてしまうのです。
≫ 【損切りできない理由】サンクコスト効果とは?具体例で解説

派生③:保有効果
保有効果とは…
現在所有している物の価値について、それを所有していなかったときよりも高く感じる現象のこと。その結果、一度手に入れたものを手放し難くなります。
一度手に入れたものを失うのは、「損失」にあたります。
「損失回避性」により、失う悲しみは、得る喜びの2倍の大きさになります。裏を返せば、手に入れたことにより、自分の中で価値が2倍に膨れ上がるのです。
保有効果の例
- リサイクルショップで買取依頼したときに、あまりの安さにショックを受ける
- 愛用していた腕時計にプレミアがついて、買ったときより高く売れるけど、売る気にならない
- 「使用した後でも返品OK」と言われて買ったけど、結局返品しない
マーケティングで応用する場合は、とりあえず本購入前に、とりあえずサービスを使わせてしまうのが効果的です。
よく見る「無料○ヶ月お試し」は、その典型例。契約のハードルを下げて間口を広げつつも、一度利用した顧客はそのサービスを手放しがくなって、継続利用してくれます。

派生④:現状維持バイアス
現状維持バイアスとは…
現在おかれた状況からの変化を嫌い、現状を維持したくなってしまう心理現象のこと。
現状を変えるということは、現在の環境を捨てて、新しい環境を手に入れることに他なりません。現在の環境を捨てることは、「損失」と見なされます。
「損失」を避けるために、ほとんどの人は保守的な考えになってしまうのです。
現状維持バイアスの例
- 転職したいと思っても、なかなか踏み出せな
- メルマガをなかなか解除しない
- 大抵の改革は失敗して現状維持路線に落ちつく。改革派よりも、失うものがある保守派の意見が強いため
ビジネスで応用する場合は、デフォルトでメルマガ登録する、契約は自動更新にするといった方法があります。一度提供してしまえば、現状維持で継続してくれる可能性が高いです。
≫ 現状維持バイアスとは?克服方法&デフォルト効果によるビジネス活用を解説

派生⑤:確実性効果
確実性効果とは…
100%確実なものに過大な価値を感じる現象のこと。
「感応度逓減性」により、利益が増えれば増えるほど、追加で感じる嬉しさが下がっていきます。そのため、一か八かで利益が吹き飛ぶくらいなら、少しくらい利益を下げてでも、確実に利益を得ようとします。
確実性効果の例
- 割高でも「ハズレなし」のくじが魅力に感じる
- 万が一にもフェイク品を摑まされたくないので、少々高くても正規店で買う
ビジネスでの典型的な活用方法は、保険サービスです。99.9%は何も起きないけど、万が一のリスクを保障することで対価を得るビジネスモデルです。
≫ アレのパラドックスとは?確実性効果を使ったビジネス活用例を解説

派生⑥:メンタルアカウンティング
メンタルアカウンティングとは…
同じお金でも、入手した方法や使い道によって色分けし、別の勘定として扱うこと。心の中には複数の帳簿があり、無意識のうちに、その帳簿ごとに使い過ぎかどうかを判断しています。
食費、光熱費、交際費などの帳簿には、それぞれ「参照点」となる基準値があります。光熱費なら月1万円、食費なら月5万円といった具合です。
それぞれの帳簿毎の参照点で、黒字か赤字かを判断します。光熱費があまりかからない春や秋だからといって、浮いたお金で3,000円のランチを食べようとはしませんよね。
ビジネスで応用する場合は、普段とは違う帳簿(お財布)を攻める策が有効です。
食費が逼迫している家庭に、ただ美味しいだけの外食をアピールしてもなびきません。記念日やデートのための外食をアピールすれば、交際費の枠からお金を使ってもらえます。
≫ 【お金に色はつきまくり】メンタルアカウンティングとは?具体例で解説

まとめ

今回は、行動経済学でもっとも有名な「プロスペクト理論」を紹介させていただきました。
プロスペクト理論とは…
- 利益や損失が確率で発生するような状況で、人間がどのような意思決定をしているかをモデル化した理論
プロスペクト理論の3原則
- 損失回避性…
損失を利益より大きく評価する現象 - 感応度逓減性…
利得・損失の絶対値が大きくなにつれて、嬉しさ・悲しさの感覚が鈍っていく現象 - 参照点依存性…
ある地点の数値を基準として、その基準値からの変化で損得を判断すること
プロスペクト理論を仕事に活かす思考法
- この1回だけではなく、何回もあるうちの1回と考える
- 損失を強調して伝える
- 不安からビジネスチャンスを見出す
- 目標値を定める
プロスペクト理論は汎用的な内容であるがゆえに、多くのシーンに活用できます。
たくさんの理論を中途半端にかじるくらいなら、プロスペクト理論だけをしっかり学んだ方が役に立ちます。ぜひ覚えておいてくださいね。
参考書籍
参考書籍は、プロスペクト理論を提唱したノーベル経済学賞受賞のダニエル・カーネマンの名著「ファスト&スロー」。
行動経済学のバイブル的な存在で、人生にもビジネスにも、応用できるヒントが目白押しです。非常にオススメの一冊です。
上下巻に分かれていて、プロスペクト理論は下巻の方ですが、理解を深めるためには上巻から読み進めていくことをオススメします。(ちょっと時間はかかりますが)
こちらは本聴き放題の「Audible」に対応しています。通勤・通学などの隙間時間で、手が塞がっていてもインプットできるので、本を読む時間が取れない人にはオススメです。
またAudibleは初回30日間無料。万が一合わなければ、解約すればコストはかかりません(それでも30日間はタダで本が聴けてしまいますが)。
本来なら聴き放題の対象になるような本ではないはず。ひょっとしたら、対象外になる日が来るかも…。早めのチェックをオススメします。
社会人の学びに「この2つ」は絶対外せない!
あらゆる教材の中で、コスパ最強なのが書籍。内容はセミナーやコンサルと遜色ないレベルなのに、なぜか1冊1,000円ほどしかかりません。
それでも数を読もうとすると、チリも積もればで結構な出費に。ハイペースで読んでいくなら、月1万円以上は覚悟しなければなりません…。
しかし現代はありがたいことに、月額で本読み放題のサービスがあります!
外せない❶ Kindle Unlimited

Amazonの電子書籍の読み放題サービス「Kindle Unlimited(キンドルアンリミテッド)」は、月額980円。本1冊分の値段で約200万冊が読み放題になります。
新刊のビジネス書が早々に読み放題になっていることも珍しくありません。個人的には、ラインナップはかなり充実していると思います。
外せない❷ Audible

こちらもAmazonの「Audible(オーディブル)」は、耳で本を聴くサービスです。月額1,500円で約12万冊が聴き放題になります。
Audibleの最大のメリットは、手が塞がっていても耳で聴けること。通勤中や家事をしながら、子供を寝かしつけながらでも学習できます。
冊数はKindle Unlimitedより少ないものの、Kindle Unlimitedにはない良書が聴き放題になっていることも多い。有料の本もありますが、無料の本だけでも十分聴き倒せます。
ちなみにわたしは両方契約しています。シーンで使い分けているのと、両者の蔵書ラインナップが被っていないためです。
どちらも30日間は無料なので、万が一読みたい本がなかった場合は解約してください(30日以内であれば、仮に何冊読んでいても無料です)。
そして読書は、早く始めた人が圧倒的に有利。本は読めば読むほど、複利のように雪だるま式に知識が蓄積されていくからです。
ガンガン読んで、ガンガン知識をつけて周りに差をつけましょう!
とりあえず両方試してみて、それぞれのラインナップをチェックするのがオススメです!